Answer:
0% probability that a customer will be exactly 7.50 minutes in the record store.
Explanation:
Uniform probability distribution:
An uniform distribution has two bounds, a and b.
The probability of finding a value of at lower than x is:
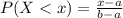
The probability of finding a value between c and d is:
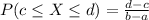
The probability of finding a value above x is:

The uniform distribution is a continuous distribution, which means that the probability of an exact outcome is zero.
Uniformly distributed between 3 and 12 minutes.
This means that
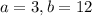
What is the probability that a customer will be exactly 7.50 minutes in the record store?
Continuous distribution, so:
0% probability that a customer will be exactly 7.50 minutes in the record store.