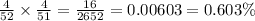Answer:
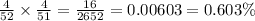
Explanation:
There are 52 cards in a standard deck, and there are 4 suits for each card. Therefore there are 4 twos and 4 tens.
At first we have 52 cards to choose from, and we need to get 1 of the 4 twos, therefore the probability is just
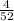
After we've chosen a two, we need to choose one of the 4 tens. But remember that we're now choosing out of a deck of just 51 cards, since one card was removed. Therefore the probability is

Now to get the total probability we need to multiply the two probabilities together