Answer:
The 95% confidence interval for the proportion of respondents who say the Internet has strengthened their relationship with family and friends is:
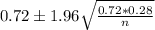
In which n is the sample size of the survey.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the z-score that has a p-value of
 .
.
The sample survey showed that 72% of Internet users said the Internet has generally strengthened their relationship with family and friends.
This means that
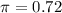
95% confidence level
So
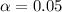 , z is the value of Z that has a p-value of
, z is the value of Z that has a p-value of
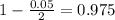 , so
, so
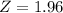 .
.
Confidence interval:

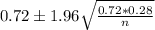
The 95% confidence interval for the proportion of respondents who say the Internet has strengthened their relationship with family and friends is:
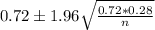
In which n is the sample size of the survey.