Question

Let f(x) = e ^3x/5x − 2. Find f'(0).

Answer 1

Explanation:

Our friend asking what the actual function is has a point. I completed this under the assumption that what we have is:

`f(x)=(e^(3x))/(5x-2)` and used the quotient rule to find the derivative, as follows:

`f'(x)=(e^(3x)(5)-[(5x-2)(3e^(3x))])/((5x-2)^2)` and simplifying a bit:

`f'(x)=(5e^(3x)-[15xe^(3x)-6e^(3x)])/((5x-2)^2)`and a bit more to:

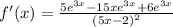`f'(x)=(5e^(3x)-15xe^(3x)+6e^(3x))/((5x-2)^2)` and combining like terms:

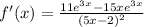`f'(x)=(11e^(3x)-15xe^(3x))/((5x-2)^2)` and factor out the GFC in the numerator to get:

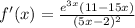`f'(x)=(e^(3x)(11-15x))/((5x-2)^2)` That's the derivative simplified. If we want f'(0), we sub in 0's for the x's in there and get the value of the derivative at x = 0:

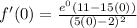`f'(0)=(e^0(11-15(0)))/((5(0)-2)^2)` which simplifies to

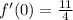`f'(0)=(11)/(4)` which translates to

The slope of the function is 11/4 at the point (0, -1/2)