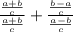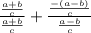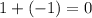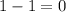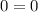Answer:
The equation is true.
Explanation:
In order to solve this problem, one must envision a right triangle. A diagram used to represent the imagined right triangle is included at the bottom of this explanation. Please note that each side is named with respect to the angle is it across from.
Right angle trigonometry is composed of a sequence of ratios that relate the sides and angles of a right triangle. These ratios are as follows,
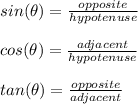
One is given the following equation,
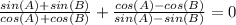
As per the attached reference image, one can state the following, using the right angle trigonometric ratios,
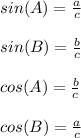
Substitute these values into the given equation. Then simplify the equation to prove the idenity,
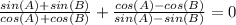
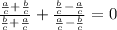
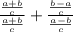
Remember, any number over itself equals one, this holds true even for fractions with fractions in the numerator (value on top of the fraction bar) and denominator (value under the fraction bar).