Question

Find the dimensions of a rectangle with perimeter 108 m whose area is as large as possible. (If both values are the same number, enter it into both blanks.) m (smaller value) m (larger value)

Answer 1

27 by 27

Explanation:

Let the sides be x and y. The problem is essentially asking:

Given 2(x+y)=108, maximize xy.

We know that x+y=54. By the Arithmetic Mean - Geometric Mean inequality, we can see that
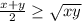`(x+y)/(2) \ge \sqrt{xy`. Substituting in x+y=54, we get
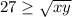`27\ge√(xy)`, meaning that
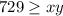`729 \ge xy`. Equality will only be obtained when x=y (in this case it will generate the maximum for xy), so setting x = y, we can see that x = y = 27. Hence, 27 is the answer you are looking for.