Answer:
Step-by-step explanation:
The formula for angular velocity is
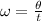 where omega is the angular velocity, theta is the change in the angular rotation, and t is the time in seconds. First and foremost, we have the angular rotation in minutes and the time in seconds, so that's a problem we have to amend. Let's change the angular rotation to rotations per second:
where omega is the angular velocity, theta is the change in the angular rotation, and t is the time in seconds. First and foremost, we have the angular rotation in minutes and the time in seconds, so that's a problem we have to amend. Let's change the angular rotation to rotations per second:
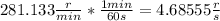
Now we're ready to set up the problem:
 and we multiply both sides by 3.686 to get the rotations per seconds:
and we multiply both sides by 3.686 to get the rotations per seconds:
θ = 17.27 rotations