Question

Helpppp please.......​

Answer 1

The equation your teacher has given you is an identity. We can prove this by transforming one side into the other. I'll transform the right hand side (RHS) into the left hand side (LHS).

This means I'll keep the LHS the same for each line. I'll only change the RHS. The goal is to get the same thing on both sides (I could go the other way around but I find this pathway is easier).

`\tan^4(\theta)+\sec^2(\theta) = \sec^4(\theta)-\tan^2(\theta)\\\\\tan^4(\theta)+\sec^2(\theta) = \left(\sec^2(\theta)\right)^2-\tan^2(\theta)\\\\\tan^4(\theta)+\sec^2(\theta) = \left(\tan^2(\theta)+1\right)^2-\tan^2(\theta) \ \text{ ... see note 1}\\\\\tan^4(\theta)+\sec^2(\theta) = \tan^4(\theta)+2\tan^2(\theta)+1-\tan^2(\theta)\\\\`

`\tan^4(\theta)+\sec^2(\theta) = \tan^4(\theta)+\tan^2(\theta)+1\\\\\tan^4(\theta)+\sec^2(\theta) = \tan^4(\theta)+\sec^2(\theta)-1+1 \ \text{ ... see note 2}\\\\\tan^4(\theta)+\sec^2(\theta) = \tan^4(\theta)+\sec^2(\theta) \ \ \Large \checkmark\\\\`

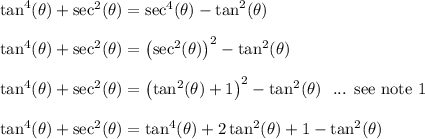
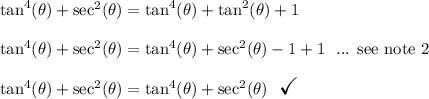
• note1: I use the identity
  `\tan^2(\theta)+1 = \sec^2(\theta)` which is derived from the pythagorean trig identity
  `\sin^2(\theta)+\cos^2(\theta) = 1`
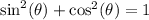
• note2: based on the previous note, we can say
  `\tan^2(\theta) = \sec^2(\theta)-1`

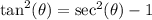
So because we've arrived at the same thing on both sides, the original equation is an identity. It always true no matter what theta value you plug in, as long as theta is in the domain. So something like theta = pi/2 won't work because tan(pi/2) = undefined and sec(pi/2) = undefined. It's based on how cos(pi/2) = 0 and this value is in the denominator. Dividing by zero is undefined.

Consequently, this means all solutions to cos(theta) = 0 will be excluded from the domain. Everything else works.