Question

Question 1 and 2 plz explain

Answer 1

1.D

2.B

Explanation:

1. The x intercept is the value of x when y is zero. We know that the x intercept is 0.5 so we must find a value of k that will make our rational function equal zero when x=0.5

`y = (k)/(x + 1) - 2`

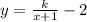
Substitute x=0.5 and y=0.

`0 = (k)/(0.5 + 1) - 2`

`0= (k)/(1.5) - 2`

`2 = (k)/(1.5)`

`3 = k`

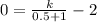
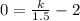
D is the Answer.

2. We need to consider the function

`\frac{2x}{1 - {x}^(2) }`

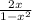
Since the numerator is a linear term, it will have one zero to the equation using fundamental Theorem of Algebra so C is wrong.

This is a rational function because we are dividing two polynomials by each other and q(x) or the denominator isnt zero. So D is wrong.

The denominator is a quadratic term so it will have two vertical asymptote according to the fundamental Theorem of Algebra So A is Wrong.

B is Right, the equation isnt defined at x=0 because when we plug 0 into the denominator, it doesn't equate to zero.