Question

A rock is dropped from a height of 100 feet calculate the time between when the rock was strong and when he landed if we choose down as positive and ignore air friction the function is h(t)=16t^2-100

Answer 1

`2.5s`

Explanation:

We are given a function which tells us at what time the rock is at a certain height. What should be the height of this function when the rock hits the ground? 0, because it has no height, it's on the ground!

So let's plug in 0, and see what value we get for the time.

`0 = 16t^2-100\\100 = 16t^2\\(100)/(16) = t^2\\`

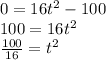
To solve for t we need to take the square root of both sides.

`t = \sqrt{(100)/(16) } = (10)/(4) = 2.5s`

Answer 2

2.5s (got the same question hope this helps :3)