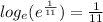Answer:
Explanation:
First, remember that the ln function is just a log function with a base of e. Here's how it looks
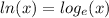
![ln(\sqrt[11]{e} ) = log_(e)(\sqrt[11]{e} )](https://img.qammunity.org/2022/formulas/mathematics/college/eml5mdeigu34h2oc1bm5n0hf8dvd0g0sqr.png)
We can take this one step further if we realize that we can rewrite the square root as a simple power to a fraction!
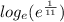
Solving the equation above is really simple. All that function is really saying is can we raise e to some number, where the result would be e^(1/11)? In other words find x.
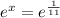
Well x has to be 1/11 in that case. And that ends up being our final answer.