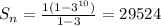Answer:
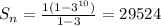
Explanation:
There's a handy formula we can use to find the sum of a geometric sequence, and here it is
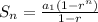
The value n represents the amount of terms you want to sum in the sequence. The variable r is known as the common ratio, and a is just some constant. Let's find those values.
First lets visualize this sequence

Okay so there's clearly a pattern here, let's write it a bit more concisely. For each n, starting at 1, we raise 3 to the (n-1) power, add it to what we had for the previous term.
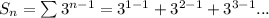
Our coefficients of r, and a, are already here! As you can see below, r is just 3, and a is just 1.
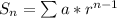
To finish up lets plug these coefficients in and get our sum after 10 terms.