Answer:

Explanation:
The graph you see there is called a parabola. The general equation for the graph is as below
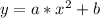
To find the equation we need to find the constants a and b. The constant b is just how much we're lifting the parabola by. Notice it's lifted by 1 on the y axis.
To find a it's a little more tricky. Let's use the graph to find a value for a by plugging in values we know. We know that b is 1 from the previous step, and we know that when x=1, y=3. Let's use that!
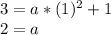
Awesome, we've found both values. And we can write the result.

I'll include a plotted graph with our equation just so you can verify it is indeed the same.