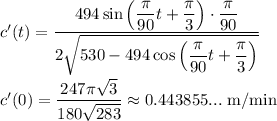9514 1404 393
Answer:
0.444 m/min
Explanation:
I find this kind of question to be answered easily by a graphing calculator.
The length of the third side can be found using the law of cosines. If the angle of interest is C, the two given sides 'a' and 'b', then the third side is ...
c = √(a² +b² -2ab·cos(C))
Since C is a function of time, its value in degrees can be written ...
C = 60° +2t° . . . . . where t is in minutes, and t=0 is the time of interest
Using a=13, and b=19, the length of the third side is ...
c(t) = √(13² +19² -2·13·19·cos(60° +2t°))
Most graphing calculators are able to compute a numerical value of the derivative of a function. Here, we use the Desmos calculator for that. (Angles are set to degrees.) It tells us the rate of change of side 'c' is ...
0.443855627418 m/min ≈ 0.444 m/min
_____
Additional comment
At that time, the length of the third side is about 16.823 m.
__
c(t) reduces to √(530 -494cos(π/90·t +π/3))
Then the derivative is ...