Question

Find HG and HI.

A. HG = 11/ square root 3 and HI = 7 square root 3
B. HG= 11 square root 3/3 and HI= 7 square root 3/3
C. HG= 11 square root 3 and HI = 23 square root 3
D. HG= 11 square root 3/3 and HI = 22 square root 3/3

Answer 1

Answer: Choice D

HG= 11 square root 3/3 and HI = 22 square root 3/3

In other words,
`\text{HG} = (11√(3))/(3) \ \text{ and } \ \text{HI} = (22√(3))/(3)\\\\`

==========================================================

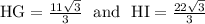
Step-by-step explanation:

Let's say that x is the short leg and y is the long leg

For any 30-60-90 triangle, we have this connection:
`y = x√(3)`

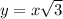
The long leg y is exactly sqrt(3) times longer compared to the short leg x.

Let's solve for x and then plug in y = 11

`y = x√(3)\\\\x = (y)/(√(3))\\\\x = (y*√(3))/(√(3)*√(3))\\\\x = (y√(3))/(3)\\\\x = (11√(3))/(3)\\\\`

Side HG, the shorter leg, has an exact length of
`\text{HG} = (11√(3))/(3)\\\\`

------------------

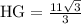
Once we know the short leg, we double that expression to get the length of the hypotenuse. Like before, this only applies to 30-60-90 triangles.

`\text{hypotenuse} = 2*(\text{short leg})\\\\\text{HI} = 2*\text{HG}\\\\\text{HI} = 2*(11√(3))/(3)\\\\\text{HI} = (22√(3))/(3)\\\\`

------------------

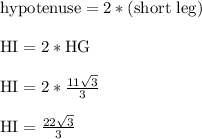
Since
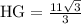`\text{HG} = (11√(3))/(3)\\\\` and
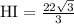`\text{HI} = (22√(3))/(3)\\\\`, this shows that choice D is the final answer.