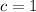Answer:
b)
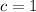
Explanation:
From the question, we are told that:
Function

Given
Rolle's theorem states that if a function f is continuous on the closed interval [a, b] and differentiable on the open interval (a, b) such that f(a) = f(b), then f′(x) = 0 for some x with a ≤ x ≤ b.
Generally, the Function above is a polynomial that can be Differentiated and it is continuous
Where
-F(x) is continuous at (-1,3)
-F(x) Can be differentiated at (-1.3)
-And F(-1)=F(3)
Therefore
F(x) has Satisfied all the Requirements for Rolle's Theorem
Differentiating F(x) we have
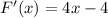
Equating F(c) we have
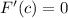
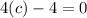
Therefore