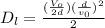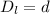Question

A uniform electric field of strength E points to the right. An electron is fired with a velocity v0 to the right and travels a distance d before coming to a stop. An second electron is then fired upwards through the same field at a velocity of v0. After the electron moving vertical has traveled vertically upwards a distance d, how far will it have moved horizontally?

Answer 1

`D_l=d`

Step-by-step explanation:

From the question we are told that:

The Electric field of strength direction =Right

The Velocity of The First Electron=V_0

The Velocity of The Second Electron=V_0

Therefore

`V_(e1)=V_(e2)`

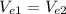
Generally, the equation for the Horizontal Displacement of electron is mathematically given by

`D=(at^2)/(2)`

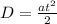
Where

Acceleration is given as

`a=(V_o)/(2d)`

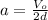
And

Time

`T=(d)/(v_0)`

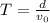
Therefore horizontal displacement towards the left is

`D_l=(((V_o)/(2d))((d)/(v_0))^2)/(2)`

`D_l=d`