Answer:
the angle between the electron's velocity and the magnetic field is 19⁰
Step-by-step explanation:
Given;
magnitude of the magnetic field, B = 83 x 10⁻⁵ T
acceleration of the electron, a = 34 x 10¹³ m/s²
speed of the electron, v = 72 x 10⁵ m/s
mass of electron, m = 9.11 x 10⁻³¹ kg
The magnetic force experienced by the electron is calculated as;
F = ma = qvB sinθ
where;
q is charge of electron = 1.602 x 10⁻¹⁹ C
θ is the angle between the electron's velocity and the magnetic field.
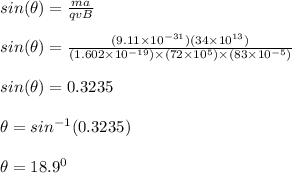

Therefore, the angle between the electron's velocity and the magnetic field is 19⁰