Question

Among various ethnic groups, the standard deviation of heights is known to be approximately three inches. We wish to construct a 95% confidence interval for the mean height of male Swedes. Forty-eight mile Swedes are surveyed. The sample mean is 71 inches. The sample standard deviation is 2.8 inches.

Required:
a. Calculate the error bound.
b. What will happen to the level of confidence obtained if 1,000 male Swedes are surveyed instead of 48? Why?

Answer 1

a) The error bound of the confidence interval is of 0.66.

b) The confidence interval will be narrower.

Explanation:

Question a:

We have to find the margin of error. Considering that we have the standard deviation for the sample, the t-distribution is used.

The first step to solve this problem is finding how many degrees of freedom,which is the sample size subtracted by 1. So

df = 71 - 1 = 70

95% confidence interval

Now, we have to find a value of T, which is found looking at the t table, with 70 degrees of freedom(y-axis) and a confidence level of
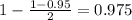`1 - (1 - 0.95)/(2) = 0.975`. So we have T = 1.9944

The margin of error is:

`M = T(s)/(√(n))`

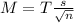
In which s is the standard deviation of the sample and n is the size of the sample.

For this problem,
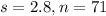`s = 2.8, n = 71`. So

`M = T(s)/(√(n)) = 1.9944(2.8)/(√(71)) = 0.66`

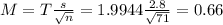
The error bound of the confidence interval is of 0.66.

b. What will happen to the level of confidence obtained if 1,000 male Swedes are surveyed instead of 48? Why?

The margin of error is inversely proportional to the square root of the sample size, so increasing the sample size leads to a smaller margin of error and a narrower confidence interval.