Answer:
a. 1.44
Explanation:
We are interested in determining whether or not the proportion of the population in favor of Candidate A is significantly more than 40%.
At the null hypothesis, it is tested if the proportion is of at most 40%, that is:
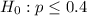
At the alternative hypothesis, it is tested if the proportion is of more than 40%, that is:
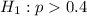
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
0.4 is tested at the null hypothesis:
This means that
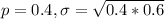
A random sample of 200 people was taken. 90 of the people in the sample favored Candidate A.
This means that:
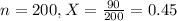
Value of the test statistic:

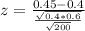
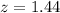
Thus the correct answer is given by option a.