Answer:
The 5-hour decay factor for the number of mg of caffeine in Ben's body is of 0.1469.
Explanation:
After consuming the energy drink, the amount of caffeine in Ben's body decreases exponentially.
This means that the amount of caffeine after t hours is given by:

In which A(0) is the initial amount and k is the decay rate, as a decimal.
The 10-hour decay factor for the number of mg of caffeine in Ben's body is 0.2722.
1 - 0.2722 = 0.7278, thus,
 . We use this to find k.
. We use this to find k.

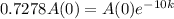
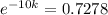
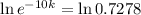
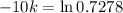
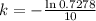
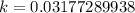
Then

What is the 5-hour growth/decay factor for the number of mg of caffeine in Ben's body?
We have to find find A(5), as a function of A(0). So
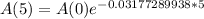
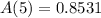
The decay factor is:
1 - 0.8531 = 0.1469
The 5-hour decay factor for the number of mg of caffeine in Ben's body is of 0.1469.