Question

A student majoring in accounting is trying to decide on the number of firms to which he should apply. Given his work experience and grades, he can expect to receive a job offer from 70% of the firms to which he applies. The student decides to apply to only four firms.

(a) What is the probability that he receives no job offer?
(b) How many job offers he expects to get?
(c) What is the probability that more than half of the firms he applied do not make him any offer?
(d) What assumptions do you need to make to find the probabilities? To increase the chance of securing more job offers, the student decides to apply to as many companies as possible, he sent out 60 applications to all different accounting firms.
(e) What is the probability of him securing more than 3 offers?

Answer 1

a) 0.0081 = 0.81% probability that he receives no job offer

b) He expects to get 2.8 job offers.

c) 0.0837 = 8.37% probability that more than half of the firms he applied do not make him any offer.

d) Each job must be independent of other jobs. Additionaly, if
`np \geq 10` and
`n(1-p) \geq 10`, the normal approximation to the binomial distribution can be used.

e) 0.2401 = 24.01% probability of him securing more than 3 offers.

Explanation:

For each application, there are only two possible outcomes. Either he gets an offer, or he does not. The probability of getting an offer for a job is independent of any other job, which means that the binomial probability distribution is used to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

He can expect to receive a job offer from 70% of the firms to which he applies.

This means that
`p = 0.7`

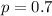
The student decides to apply to only four firms.

This means that
`n = 4`

(a) What is the probability that he receives no job offer?

This is
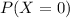`P(X = 0)`. So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(4,0).(0.7)^(0).(0.3)^(4) = 0.0081`

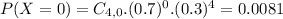
0.0081 = 0.81% probability that he receives no job offer.

(b) How many job offers he expects to get?

The expected value of the binomial distribution is:

`E(X) = np`

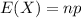
In this question:

`E(X) = 4(0.7) = 2.8`

He expects to get 2.8 job offers.

(c) What is the probability that more than half of the firms he applied do not make him any offer?

Less than 2 offers, which is:

`P(X < 2) = P(X = 0) + P(X = 1)`

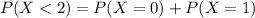
So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(4,0).(0.7)^(0).(0.3)^(4) = 0.0081`

`P(X = 1) = C_(4,1).(0.7)^(1).(0.3)^(3) = 0.0756`

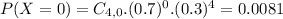
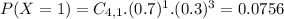
Then

`P(X < 2) = P(X = 0) + P(X = 1) = 0.0081 + 0.0756 = 0.0837`

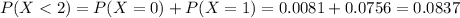
0.0837 = 8.37% probability that more than half of the firms he applied do not make him any offer.

(d) What assumptions do you need to make to find the probabilities? To increase the chance of securing more job offers, the student decides to apply to as many companies as possible, he sent out 60 applications to all different accounting firms.

Each job must be independent of other jobs. Additionaly, if
`np \geq 10` and
`n(1-p) \geq 10`, the normal approximation to the binomial distribution can be used.

(e) What is the probability of him securing more than 3 offers?

Between 4 and n, since n is 4, 4 offers, so:

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 4) = C_(4,4).(0.7)^(4).(0.3)^(0) = 0.2401`

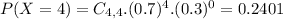
0.2401 = 24.01% probability of him securing more than 3 offers.