Question

An electron is released from rest at a distance of 9.00 cm from a fixed proton. How fast will the electron be moving when it is 3.00 cm from the proton

Answer 1

the speed of the electron at the given position is 106.2 m/s

Step-by-step explanation:

Given;

initial position of the electron, r = 9 cm = 0.09 m

final position of the electron, r₂ = 3 cm = 0.03 m

let the speed of the electron at the given position = v

The initial potential energy of the electron is calculated as;

`U_i = Fr = (kq^2)/(r^2) * r = (kq^2)/(r) \\\\U_i = ((9* 10^9)(1.602* 10^(-19))^2)/(0.09) \\\\U_i = 2.566 * 10^(-27) \ J`

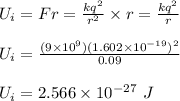
When the electron is 3 cm from the proton, the final potential energy of the electron is calculated as;

`U_f = (kq^2)/(r_2) \\\\U_f = [((9* 10^9)* (1.602 * 10^(-19))^2)/(0.03) ]\\\\U_f = 7.669 * 10^(-27) \ J \\\\\Delta U = U_f -U_i\\\\\Delta U = (7.699* 10^(-27) \ J ) - (2.566 * 10^(-27) \ J)\\\\\Delta U = 5.133 * 10^(-27) \ J`

Apply the principle of conservation of energy;

ΔK.E = ΔU

`K.E_f -K.E_i = \Delta U\\\\initial \ velocity \ of \ the \ electron = 0\\\\K.E_f - 0 = \Delta U\\\\K.E_f = \Delta U\\\\(1)/(2) mv^2 = \Delta U\\\\where;\\\\m \ is \ the \ mass \ of\ the \ electron = 9.1 1 * 10^(-31) \ kg\\\\v^2 = ( 2 \Delta U)/(m) \\\\v = \sqrt{( 2 \Delta U)/(m)} \\\\v = \sqrt{( 2 (5.133* 10^(-27)))/(9.11* 10^(-31))}\\\\v = √(11268.935) \\\\v = 106.2 \ m/s`

Therefore, the speed of the electron at the given position is 106.2 m/s