Answer:
(a)The probability that both marbles are blue=5/18
The probability that both marbles are yellow=1/6
(b)The probability that exactly one marble is blue=5/9
Explanation:
Blue marbles=5
Yellow marbles=4
Total marbles=5+4=9
(a)
Probability of drawing first blue marble=5/9
Probability of drawing second blue marble without replacement=4/8
The probability that both marbles are blue

Probability of drawing first yellow marble=4/9
Probability of drawing second yellow marble without replacement=3/8
The probability that both marbles are yellow
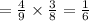
(b)
The probability that exactly one marble is blue
=Probability of first blue marble (Probability of second yellow marble)+Probability of first yellow marble (Probability of second blue marble)
The probability that exactly one marble is blue
=
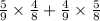
=
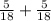
=
