Question

At a local company, 15% of the employees are women. every day, 9% of them bring their lunch to work, while only 3% of the men bring lunch. Find the probability that a randomly selected employee

a. is a woman goven that the person brings their lunch to work.
b. brings their lunch to work given that person is a woman.
c. is a woman given that the person brings their lunch to work.

Answer 1

a) 0.3462 = 34.62% that a randomly selected employee is a woman given that the person brings their lunch to work.

b) 0.09 = 9% probability that a randomly selected employee brings their lunch to work given that person is a woman.

c) 0.3462 = 34.62% that a randomly selected employee is a woman given that the person brings their lunch to work.

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

Questions a/c:

Questions a and c are the same, so:

Event A: Brings lunch to work.

Event B: Is a woman.

Probability of a person bringing lunch to work:

9% of 15%(woman)

3% of 100 - 15 = 85%(man). So

`P(A) = 0.09*0.15 + 0.03*0.85 = 0.039`

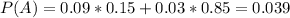
Probability of a person bringing lunch to work and being a woman:

9% of 15%, so:

`P(A \cap B) = 0.09*0.15`

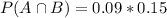
Desired probability:

`P(B|A) = (P(A \cap B))/(P(A)) = (0.09*0.15)/(0.039) = 0.3462`

0.3462 = 34.62% that a randomly selected employee is a woman given that the person brings their lunch to work.

Question b:

Event A: Woman

Event B: Brings lunch

15% of the employees are women.

This means that
`P(A) = 0.15`

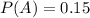
Probability of a person bringing lunch to work and being a woman:

9% of 15%, so:

`P(A \cap B) = 0.09*0.15`

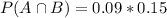
Desired probability:

`P(B|A) = (P(A \cap B))/(P(A)) = (0.09*0.15)/(0.15) = 0.09`

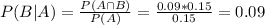
0.09 = 9% probability that a randomly selected employee brings their lunch to work given that person is a woman.