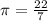Answer:
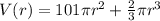
Explanation:
Given
Shapes: cylinder and hemisphere
 --- height of cylinder
--- height of cylinder
Required
The volume of the silo
The volume is calculated as:
Volume (V) = Volume of cylinder (V1) + Volume of hemisphere (V2)
So, we have:
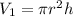
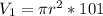
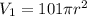 --- cylinder
--- cylinder
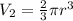 ---- hemisphere
---- hemisphere
So, the volume of the silo is:
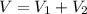
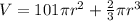
Write as a function
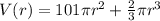
Where: