Answer:
The sample size needed is of 10,484.
Explanation:
We have to find our
 level, that is the subtraction of 1 by the confidence interval divided by 2. So:
level, that is the subtraction of 1 by the confidence interval divided by 2. So:
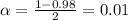
Now, we have to find z in the Z-table as such z has a p-value of
 .
.
That is z with a p-value of
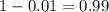 , so Z = 2.327.
, so Z = 2.327.
Now, find the margin of error M as such

In which
 is the standard deviation of the population and n is the size of the sample.
is the standard deviation of the population and n is the size of the sample.
The weekly earnings of students in one age group are normally distributed with a standard deviation of 88 dollars.
This means that
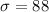
Find the sample size needed to assure with 98 percent confidence that the sample mean will not differ from the population mean by more than 2 dollars.
This is n for which M = 2. So

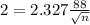
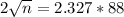
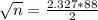
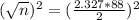
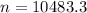
Rounding up:
The sample size needed is of 10,484.