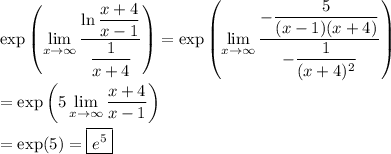Question

Lim ₓ→∞ (x+4/x-1)∧x+4​

Answer 1

It looks like the limit you want to find is

`\displaystyle \lim_(x\to\infty) \left((x+4)/(x-1)\right)^(x+4)`

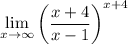
One way to compute this limit relies only on the definition of the constant e and some basic properties of limits. In particular,

`e = \displaystyle\lim_(x\to\infty)\left(1+\frac1x\right)^x`

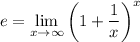
The idea is to recast the given limit to make it resemble this definition. The definition contains a fraction with x as its denominator. If we expand the fraction in the given limand, we have a denominator of x - 1. So we rewrite everything in terms of x - 1 :

`\left((x+4)/(x-1)\right)^(x+4) = \left((x-1+5)/(x-1)\right)^(x-1+5) \\\\ = \left(1+\frac5{x-1}\right)^(x-1+5) \\\\ =\left(1+\frac5{x-1}\right)^(x-1) * \left(1+\frac5{x-1}\right)^5`

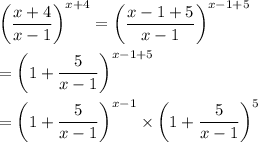
Now in the first term of this product, we substitute y = (x - 1)/5 :

`\left((x+4)/(x-1)\right)^(x+4) = \left(1+\frac1y\right)^(5y) * \left(1+\frac5{x-1}\right)^5`

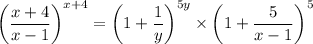
Then use a property of exponentiation to write this as

`\left((x+4)/(x-1)\right)^(x+4) = \left(\left(1+\frac1y\right)^y\right)^5 * \left(1+\frac5{x-1}\right)^5`

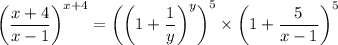
In terms of end behavior, (x - 1)/5 and x behave the same way because they both approach ∞ at a proportional rate, so we can essentially y with x. Then by applying some limit properties, we have

`\displaystyle \lim_(x\to\infty) \left((x+4)/(x-1)\right)^(x+4) = \lim_(x\to\infty) \left(\left(1+\frac1x\right)^x\right)^5 * \left(1+\frac5{x-1}\right)^5 \\\\ = \lim_(x\to\infty)\left(\left(1+\frac1x\right)^x\right)^5 * \lim_(x\to\infty)\left(1+\frac5{x-1}\right)^5 \\\\ =\left(\lim_(x\to\infty)\left(1+\frac1x\right)^x\right)^5 * \left(\lim_(x\to\infty)\left(1+\frac5{x-1}\right)\right)^5`

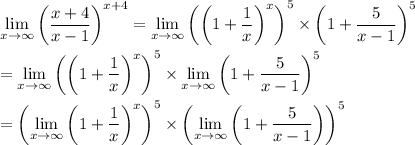
By definition, the first limit is e and the second limit is 1, so that

`\displaystyle \lim_(x\to\infty) \left((x+4)/(x-1)\right)^(x+4) = e^5*1^5 = \boxed{e^5}`

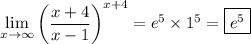
You can also use L'Hopital's rule to compute it. Evaluating the limit "directly" at infinity results in the indeterminate form
`1^\infty`.

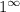Rewrite

`\left((x+4)/(x-1)\right)^(x+4) = \exp\left((x+4)\ln(x+4)/(x-1)\right)`

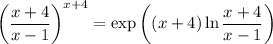
so that

`\displaystyle \lim_(x\to\infty) \left((x+4)/(x-1)\right)^(x+4) = \lim_(x\to\infty)\exp\left((x+4)\ln(x+4)/(x-1)\right) \\\\ = \exp\left(\lim_(x\to\infty)(x+4)\ln(x+4)/(x-1)\right) \\\\ =\exp\left(\lim_(x\to\infty)\frac{\ln(x+4)/(x-1)}{\frac1{x+4}}\right)`

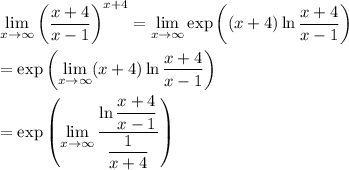
and now evaluating "directly" at infinity gives the indeterminate form 0/0, making the limit ready for L'Hopital's rule.

We have

`(\mathrm d)/(\mathrm dx)\left[\ln(x+4)/(x-1)\right] = -\frac5{(x-1)^2}*(1)/((x+4)/(x-1)) = -\frac5{(x-1)(x+4)}`

`(\mathrm d)/(\mathrm dx)\left[\frac1{x+4}\right]=-\frac1{(x+4)^2}`

and so

`\displaystyle \exp\left(\lim_(x\to\infty)\frac{\ln(x+4)/(x-1)}{\frac1{x+4}}\right) = \exp\left(\lim_(x\to\infty)\frac{-\frac5{(x-1)(x+4)}}{-\frac1{(x+4)^2}}\right) \\\\ = \exp\left(5\lim_(x\to\infty)(x+4)/(x-1)\right) \\\\ = \exp(5) = \boxed{e^5}`