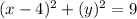Question

I AM GIVING BRAINLISEST AND 20 POINTS! Write the equation of the circle in standard form.

Answer 1

`(x-4)^2+(y)^2=9`

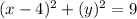
Explanation:

The general format for the equation of a circle is the following:

`(x-n)^2+(y-m)^2=a`

This circle will have a radius of (
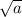`√(a)`), moreover, this circle will have its center at point
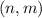`(n,m)`. Please note that its center is shifted (n) units to the right of the origin, and (m) units up. Apply this knowledge to the given problem.

The circle in the given problem has its center at (4, 0). Therefore the following can be stated,

`n=4\\\\m =0`

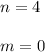
Since one knows the center of the circle is at (4, 0), and (the circle has (4, 3) on its circumference, the distance between the coordinates will produce the radius of the circle. The following formula can be used to find the distance between two points on a number line,

`D=√((x_1-x_2)^2+(y_1-y_2)^2)`

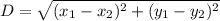
Where (
`(x_1,y_1)`) and (
`(x_2,y_2)`) are the points one is trying to find the distance between. Substitute the given points into the formula and solve for the distance between them.

`D=√((x_1-x_2)^2+(y_1-y_2)^2)`

`D=√((4-4)^2+(3-0)^2)`

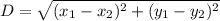
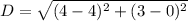
Simplify,

`D=√((4-4)^2+(3-0)^2)`

`D=√((0)^2+(3)^2)`

`D=√(0+9)`

`D=√(9)`

`D=3`

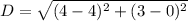
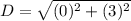
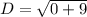
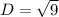
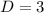
The parameter (a) is equal to (
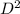`D^2`) are per the format of the equation, thus one must do the following to find the value of (a):

`a = D^2`

`a=3^3`

`a = 9`

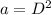
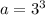
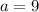
Substitute all of the information into the general formula for the equation of a circle, then simplify,

`(x-n)^2+(y-m)^2=a`

`(x-4)^2+(y-0)^2=9`

`(x-4)^2+(y)^2=9`