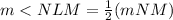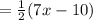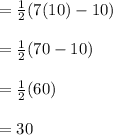Question

WILL GIVE BRAINLISEST Solve for m∠NLM



GOOD LUCKJ!

Answer 1

`m<NLM = 30`

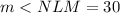
Explanation:

1. Approach

The easiest way to solve this problem is to find the degree measure of the parameter (x). Use the fact that line (LN) is a diameter to solve for (x), beacause the angle measure of a circle on either side of the diameter is (180) degrees. One can then find the measure of arc (mNM), and then find the measure of the angle (<NLM) using the inscribed angles theory.

2. Find the measure of (x)

A diameter is the largest chord or segment in a circle. It intersects a circle at two points and runs through the center of a circle. The degree measure of a circle on either side of the diameter is (180) degrees. As per the given image, line (LN) is a diameter. The arcs (mLM) and (mNM) make up half of the circle, or rather one side of the diameter. With this information, one can form an equation and solve for the parameter (x) using this information:

`(mLM)+(mNM)=180`

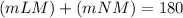
Substitute,

`(mLM)+(mNM)=180`

`(13x-10)+(7x-10)=180`

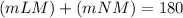
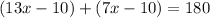
Simplify,

`(13x-10)+(7x-10)=180`

`20x-20=180`

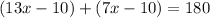
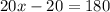
Inverse operations,

`20x-20=180`

`20x=200`

`x=10`

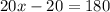
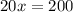
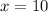
3. Find the measure of angle (<NLM)

The inscribed angles theorem states that an angle with its vertex on the circumference (outer edge) of a circle is equal to half of the surrounding arc. One can form an equation and solve for the measure of angle (<NLM).

`m<NLM=(1)/(2)(mNM)`

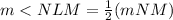
Substitute,

`m<NLM=(1)/(2)(mNM)`

`=(1)/(2)(7x-10)`

`=(1)/(2)(7(10)-10)\\\\=(1)/(2)(70-10)\\\\=(1)/(2)(60)\\\\=30`