Question

Anyone know collage level algebra 2? I need help

Evaluate the series: image Question 1 options: A) 392 B) 249 C) 420 D) 406

Answer 1

The required sum is 392

Explanation:

Given the sum as shown;

`\sum \left \77} \atop {a=1}} \right. (3a^2-4)`

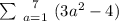
When n = 1

f(1) = 3(1)²-4

f(1) = 3 - 4

f(1) = - 1

When n = 2

f(2) = 3(2)²-4

f(2) = 12 - 4

f(2) = 8

When n = 3

f(3) = 3(3)²-4

f(3) = 27 - 4

f(3) = 23

When n = 4

f(4) = 3(4)²-4

f(4) = 48 - 4

f(4) = 44

When n = 5

f(5) = 3(5)²-4

f(5) = 75 - 4

f(5) = 71

When n = 6

f(6) = 3(6)²-4

f(6) = 108 - 4

f(6) = 104

When n = 7

f(7) = 3(7)²-4

f(7) = 147 - 4

f(7) = 143

Taking their sum

Sum = f(1)+f(2)+(3)+f(4)+f(5)+f(6)+f(7)

Sum = -1 + 8 + 23 + 44 + 71 + 104 + 143

Sum = 392

Hence the required sum is 392