Answer:
Answer: Option A.
Explanation:
Hey there!
Given; The Line BC contains points B (4, -5) and C (3, 2).
And the Line DE contains points D (2,0) and E (9, 1)
Note: Use double point formula for finding the equation and then find slopes of both then put the condition for perpendicular lines and parallel lines.
From line BC;
The points are B (4, -5) and C (3, 2).
Using double point formula;

Keep all the value;
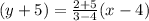
Simplify it;
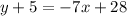
Therefore, the equation is y = -7x+23........(I)And slope(m1) is -7 {comparing the equation (I) with y=Mx+c}
Again;
The points D (2,0) and E (9, 1)
Using double point formula;
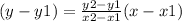
Keep all values;
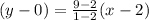
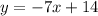
Therefore, the equation is y = -7x+14......(ii)And the slope (m2) is -7. {comparing the equation (ii) with y= mx+c}
Check:
For parallel lines:
m1= m2
-7 = -7 (true)
Therefore, the lines are parallel.
Hope it helps!