Question

find k so that x^2+2x+k is a factor of 2x^4+x^3-14x^2+5x+6. also find all the zeroes of the two polynomial​

Answer 1

Compute the quotient and remainder,

`(2x^4+x^3-14x^2+5x+6)/(x^2+2x+k) \\\\ = 2x^2 - 3x - (8+2k) + ((21+7k)x+(6+8k+2k^2))/(x^2+2x+k)`

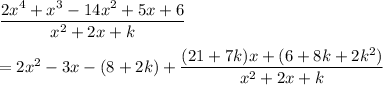
The remainder upon dividing
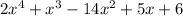`2x^4+x^3-14x^2+5x+6` by
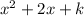`x^2+2x+k` should leave no remainder, which means

`21+7k = 0 \implies 21 = -7k \implies k=-3`

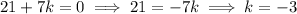
and

`6+8k+2k^2 = 0 \implies 2(k+3)(k+1)=0 \implies k=-3\text{ or }k=-1`

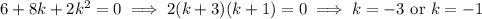
Only k = -3 makes both remainder terms vanish.

Then the previous result reduces to

`(2x^4+x^3-14x^2+5x+6)/(x^2+2x-3) = 2x^2 - 3x - 2`

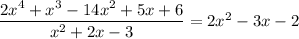
so that

`2x^4+x^3-14x^2+5x+6 = (x^2+2x-3) (2x^2 - 3x - 2) \\\\ 2x^4+x^3-14x^2+5x+6 = (x+3)(x-1)(2x + 1)(x-2)`

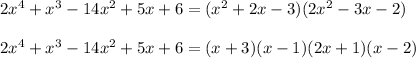
and so the zeroes of the quartic polynomial are x = -3, x = 1, x = -1/2, and x = 2.