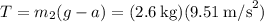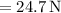Question

19 point please please answer right need help

Block on an incline
A block of mass m1 = 3.9 kg on a smooth inclined plane of angle 38is connected by a cord over a small frictionless
pulley to a second block of mass m2 = 2.6 kg hanging vertically. Take the positive direction up the incline and use 9.81
m/s2 for g.
What is the tension in the cord to the nearest whole number?

Answer 1

Step-by-step explanation:

We can write Newton's 2nd law as applied to the sliding mass
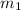`m_1` as

`T - m_1g\sin38 = m_1a\:\:\:\:\:\:\:(1)`

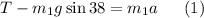
For the hanging mass
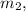`m_2,` we can write NSL as

`T - m_2g = -m_2a\:\:\:\:\:\:\:(2)`

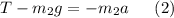
We need to solve for a first before we can solve the tension T. So combining Eqns(1) & (2), we get

`(m_1 + m_2)a = m_2g - m_1g\sin38`

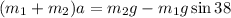
or

`a = \left((m_2 - m_1\sin38)/(m_1 + m_2)\right)g`

`\:\:\:\:= 0.30\:\text{m/s}^2`

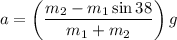
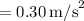
Using this value for the acceleration on Eqn(2), we find that the tension T is

`T = m_2(g - a) = (2.6\:\text{kg})(9.51\:\text{m/s}^2)`

`\:\:\:\:=24.7\:\text{N}`