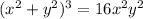Answer:
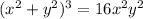
Explanation:
We want to convert the polar equation:
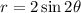
To rectangular form.
Recall the double-angle identity for sine:
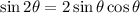
Hence:
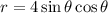
Since x = rcosθ and y = rsinθ:

Multiply:
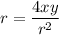
Recall that x² + y² = r². Hence:
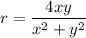
By squaring both sides:
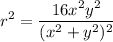
Substitute:

And multiply. Therefore: