Answer: Choice A
y=2x+3; y=-1/3x+3
==================================================
Step-by-step explanation:
The left portion of the blue curve is y = 2x+3 but it is only graphed when x < 0 (we could argue that
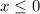 but I'll set that aside for the other portion).
but I'll set that aside for the other portion).
The right portion is the line y = -1/3x + 3 and it's only graphed when

So we could have this piecewise function
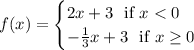
Or we could easily swap the "or equal to" portion to move to the first part instead like this
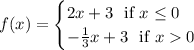
Either way, we're involving the equations mentioned in choice A