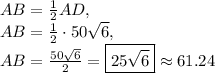Answer:
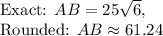
Explanation:
We can use the Law of Sines to find segment AD, which happens to be a leg of
 and the hypotenuse of
and the hypotenuse of
 .
.
The Law of Sines states that the ratio of any angle of a triangle and its opposite side is maintained through the triangle:
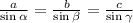
Since we're given the length of CD, we want to find the measure of the angle opposite to CD, which is
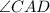 . The sum of the interior angles in a triangle is equal to 180 degrees. Thus, we have:
. The sum of the interior angles in a triangle is equal to 180 degrees. Thus, we have:
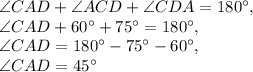
Now use this value in the Law of Sines to find AD:
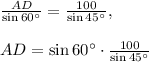
Recall that
 and
and
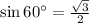 :
:
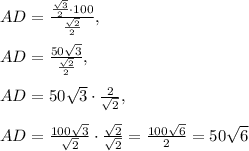
Now that we have the length of AD, we can find the length of AB. The right triangle
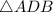 is a 30-60-90 triangle. In all 30-60-90 triangles, the side lengths are in the ratio
is a 30-60-90 triangle. In all 30-60-90 triangles, the side lengths are in the ratio
 , where
, where
 is the side opposite to the 30 degree angle and
is the side opposite to the 30 degree angle and
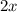 is the length of the hypotenuse.
is the length of the hypotenuse.
Since AD is the hypotenuse, it must represent
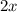 in this ratio and since AB is the side opposite to the 30 degree angle, it must represent
in this ratio and since AB is the side opposite to the 30 degree angle, it must represent
 in this ratio (Derive from basic trig for a right triangle and
in this ratio (Derive from basic trig for a right triangle and
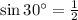 ).
).
Therefore, AB must be exactly half of AD: