Question

Alex is twice as old as Bernard and Calvin is 8 years younger than Alex. If the sum of their ages is 52, how old are they?​

Answer 1

Currently, Alex is 32 years old. His son is 8 years old,

Solution: denote the age of Alex’s son as ‘x’. Alex’s age is 4x

In 16 years, Alex’s age will be 4x + 16. His son’s age will be x + 16

4x + 16 = 2(x+16). solving this equation yields:

4x + 16 = 2x + 32. Grouping like terms algebraically gives: 2x = 16

Thus x = 16/2 = 8. 4(8) = 32

Answer 2

Alex is 24, Bernard is 12, and Calvin is 16.

Explanation:

Let Alex's age be A, Bernard's age be B, and Calvin's age be C.

We can write equations to model each situation.

Alex is twice as old as Bernard. In other words:

`A=2B`

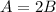
Calvin is eight year younger than Alex. In other words:

`C = A - 8`

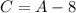
And the sum of all their ages is 52. Therefore:

`A + B + C = 52`

This is a triple system of equations. We can solve it by substitution. Substitution A and C:

`(2B)+B+(A-8)= 52`

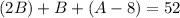
Substitute:

`2B+ B + (2B) -8 = 52`

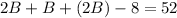
Combine like terms:

`5B-8=52`

Solve for B. Add 8 to both sides:

`5B = 60`

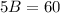
And divide both sides by five:

`B=12`

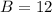
Therefore, Bernard is 12 years old.

Since Alex is twice as old as Bernard, Alex must be 24 years old.

And since Calvin is eight years younger than Alex, Calvin is 16.

In conclusion, Alex is 24, Bernard is 12, and Calvin is 16.