Answer:

Explanation:
We are asked to find x, a missing side in a triangle.
This is a right triangle because there is a small square in the corner representing a 90 degree or right angle. Therefore, we can use right triangle trigonometry. The three main functions are:
- sinθ= opposite/hypotenuse
- cosθ= adjacent/hypotenuse
- tanθ= opposite/adjacent
Examine the triangle. We will use angle S, measuring 54 degrees, for theta. Side QR, measuring x, is opposite angle S. Side QS, measuring 2.3, is the hypotenuse because it is opposite the right angle. Since we have the opposite and hypotenuse, we will use sine.
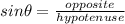
- θ= 54
- opposite= x
- hypotenuse = 2.3
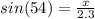
We are solving for x, so we must isolate the variable. It is being divided by 2.3 The inverse operation of division is multiplication, so we multiply both sides by 2.3
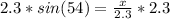
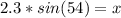
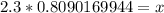
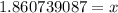
Round to the nearest tenth. The 6 in the hundredth place to the right tells us to round the 8 up to a 9.
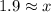
x is approximately 1.9