Answer:
Part A)
About 0.51% per year.
Part B)
About 0.30% per year.
Part C)
About 28.26%.
Explanation:
We are given that the population of Americans age 55 and older as a percentange of the total population is approximated by the function:
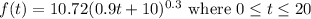
Where t is measured in years with t = 0 being the year 2000.
Part A)
Recall that the rate of change of a function at a point is given by its derivative. Thus, find the derivative of our function:
![\displaystyle f'(t) = (d)/(dt) \left[ 10.72\left(0.9t+10\right)^(0.3)\right]](https://img.qammunity.org/2022/formulas/mathematics/college/1j2so86hrfr80f1mn3abx4b5xf3gg5tnnb.png)
Rewrite:
![\displaystyle f'(t) = 10.72(d)/(dt) \left[(0.9t+10)^(0.3)\right]](https://img.qammunity.org/2022/formulas/mathematics/college/kpad0wm2ypfcak68v5jguvljqpd3njrvbx.png)
We can use the chain rule. Recall that:
![\displaystyle (d)/(dx) [u(v(x))] = u'(v(x)) \cdot v'(x)](https://img.qammunity.org/2022/formulas/mathematics/college/sn9l3ye6h58fmn3ar3mmzx67255at2xfxg.png)
Let:
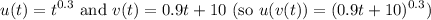
Then from the Power Rule:

Thus:
![\displaystyle (d)/(dt)\left[(0.9t+10)^(0.3)\right]= 0.3(0.9t+10)^(-0.7)\cdot 0.9](https://img.qammunity.org/2022/formulas/mathematics/college/qej9ep1c20d66q5ux6f6iclwgdn0otbzoa.png)
Substitute:
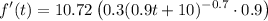
And simplify:
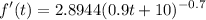
For 2002, t = 2. Then the rate at which the percentage is changing will be:

Contextually, this means the percentage is increasing by about 0.51% per year.
Part B)
Evaluate f'(t) when t = 17. This yields:
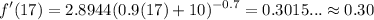
Contextually, this means the percetange is increasing by about 0.30% per year.
Part C)
For this question, we will simply use the original function since it outputs the percentage of the American population 55 and older. Thus, evaluate f(t) when t = 17:
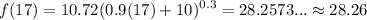
So, about 28.26% of the American population in 2017 are age 55 and older.