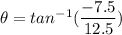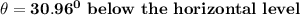Question

A stone with a mass of 0.100kg rests on a frictionless, horizontal surface. A bullet of mass 2.50g traveling horizontally at 500m/s strikes the stone and rebounds horizontally at right angles to its original direction with a speed of 300m/s.

A) Compute the magnitude of the velocity of the stone after it is struck.
B) Compute the direction of the velocity of the stone after it is struck. (degrees from the initial direction of the bullet)

Answer 1

Step-by-step explanation:

Given that:

mass of stone (M) = 0.100 kg

mass of bullet (m) = 2.50 g = 2.5 ×10 ⁻³ kg

initial velocity of stone (
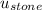`u_(stone)`) = 0 m/s

Initial velocity of bullet (
`u_(bullet)`) = (500 m/s)i

Speed of the bullet after collision (
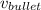`v_(bullet)`) = (300 m/s) j

Suppose we represent
`(v_(stone))` to be the velocity of the stone after the truck, then:

From linear momentum, the law of conservation can be applied which is expressed as:

`m*u_(bullet) + M*{u_(stone)}= mv_(bullet)+Mv_(stone)`

`(2.50*10^(-3) \ kg) (500)i+0 = (2.50*10^(-3) \ kg)(300 \ m/s)j + (0.100 \ kg)v_(stone)`

`(2.50*10^(-3) \ kg) (500)i- (2.50*10^(-3) \ kg)(300 \ m/s)j= (0.100 \ kg)v_(stone)`

`v_(stone)= (1.25\ kg.m/s)i-(0.75\ kg m/s)j`

`v_(stone)= (12.5\ m/s)i-(7.5\ m/s)j`

∴

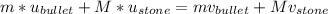
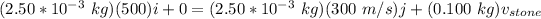
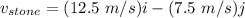
The magnitude now is:

`v_(stone)=√( (12.5\ m/s)^2-(7.5\ m/s)^2)`

`\mathbf{v_(stone)= 14.6 \ m/s}`

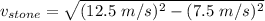
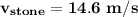
Using the tangent of an angle to determine the direction of the velocity after the struck;

Let θ represent the direction:

`\theta = tan^(-1) ((-7.5)/(12.5))`

`\mathbf{\theta = 30.96^0 \ below \ the \ horizontal\ level}`