Question

A study was conducted in order to estimate ?, the mean number of weekly hours that U.S. adults use computers at home. Suppose a random sample of 81 U.S. adults gives a mean weekly computer usage time of 8.5 hours and that from prior studies, the population standard deviation is assumed to be ? = 3.6 hours.

A similar study conducted a year earlier estimated that ?, the mean number of weekly hours that U.S. adults use computers at home, was 8 hours. We would like to test (at the usual significance level of 5%) whether the current study provides significant evidence that this mean has changed since the previous year.
Using a 95% confidence interval of (7.7, 9.3), our conclusion is that:
a. the current study does provide significant evidence that the mean number of weekly hours has changed over the past year, since 8 falls outside the confidence interval.
b. the current study does not provide significant evidence that the mean number of weekly hours has changed over the past year, since 8 falls outside the confidence interval.
c. the current study does provide significant evidence that the mean number of weekly hours has changed over the past year, since 8 falls inside the confidence interval.
d. the current study does not provide significant evidence that the mean number of weekly hours has changed over the past year, since 8 falls inside the confidence interval.
e. None of the above. The only way to reach a conclusion is by finding the p-value of the test.

Answer 1

d. the current study does not provide significant evidence that the mean number of weekly hours has changed over the past year, since 8 falls inside the confidence interval.

Explanation:

Mean was of 8 hours, test if it has changed:

At the null hypothesis, we test if it has not changed, that is, the mean is still of 8, so:

`H_0: \mu = 8`

At the alternative hypothesis, we test if it has changed, that is, the mean is different of 8, so:

`H_1: \mu \\eq 8`

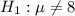
Using a 95% confidence interval of (7.7, 9.3), our conclusion is that:

8 is part of the confidence interval, which means that the study does not provide evidence that the mean has changed, and the correct answer is given by option d.