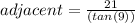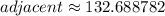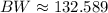1 Answer

Tempus · Answer 1 · 2022-11-21T14:31:58+0000

Answer:

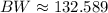
$BW \approx 132.589$

Explanation:

The given triangle (BWS) is a right triangle. This is indicated by the box around one of its angles, signifying that it is a right angle. One property of a right triangle is the right angle trigonometric ratios. These are a set of ratios that can be used to describe the relationship between the sides and angles in a triangle. These ratios are as follows:

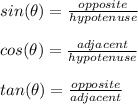
$sin(\theta) = (opposite)/(hypotenuse)\\\\cos(\theta)=(adjacent)/(hypotenuse)\\\\tan(\theta)=(opposite)/(adjacent)$

Please note that the (opposite) and (adjacent) sides are subjective, the sides that are named these terms depend on the angle of reference. However the term (hypotenuse) refers to the sides opposite the right angle of a right triangle, this term is the same no matter the angle used in the ratio.

In this case, one is given the length of the side (SB) and the measure of angle (<W), one is asked to find the length of the side (BW). The best ratio to use in this case is the ratio tangent (tan).

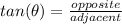
$tan(\theta)=(opposite)/(adjacent)$