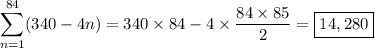The first term in the series is 336. The second term is obtained by subtracting 4 from the first term; subtract 4 from that to get the third term; and so on. Then the n-th term in the series is
336 - 4 (n - 1)
or
340 - 4n
The last term in this series is 4, so we solve for n :
340 - 4n = 4
336 = 4n
n = 336/4 = 84
The sum of the series is then
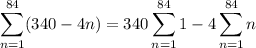
Recall that
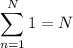
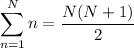
Then the sum we want is