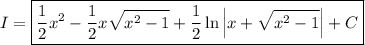Question

Integral of 1 /x+ sq.root x^2-1

Answer 1

I'm assuming the integral is

`\displaystyle \int (\mathrm dx)/(x+√(x^2-1))`

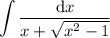
Rationalize the denominator:

`\frac1{x+√(x^2-1)} * (x-√(x^2-1))/(x-√(x^2-1)) = (x-√(x^2-1))/(x^2-\left(√(x^2-1)\right)^2) = x-√(x^2-1)`

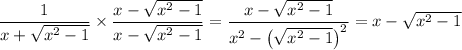
Then the integral is

`\displaystyle \int\left(x-√(x^2-1)\right)\,\mathrm dx = \frac12x^2 - \int√(x^2-1)\,\mathrm dx`

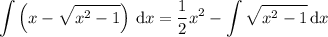
For the remaining integral, substitute x = sec(t ) and dx = sec(t ) tan(t ) dt. Then over an appropriate domain, we have

`\displaystyle\int√(x^2-1)\,\mathrm dx = \int\sec(t)\tan(t)√(\sec^2(t)-1)\,\mathrm dt = \int\sec(t)\tan^2(t)\,\mathrm dt`

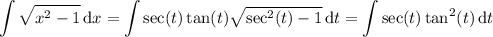
Integrate by parts, taking

u = tan(t ) ==> du = sec²(t ) dt

dv = sec(t ) tan(t ) dt ==> v = sec(t )

Then

`\displaystyle\int\sec(t)\tan^2(t)\,\mathrm dt = \sec(t)\tan(t) - \int\sec^3(t)\,\mathrm dt`

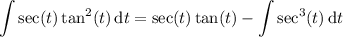
Now for *this* remaining integral, integrate by parts again, taking

u = sec(t ) ==> du = sec(t ) tan(t ) dt

dv = sec²(t ) dt ==> v = tan(t )

so that

`\displaystyle\int\sec^3(t)\,\mathrm dt = \sec(t)\tan(t) - \int\sec(t)\tan^2(t)\,\mathrm dt \\\\ \int\sec^3(t)\,\mathrm dt = \sec(t)\tan(t) - \int\sec(t)(\sec^2(t)-1)\,\mathrm dt \\\\ \int\sec^3(t)\,\mathrm dt = \sec(t)\tan(t) - \int\sec^3(t)\,\mathrm dt + \int\sec(t)\,\mathrm dt \\\\ \int\sec^3(t)\,\mathrm dt = \frac12\sec(t)\tan(t)+\frac12\int\sec(t)\,\mathrm dt \\\\ \int\sec^3(t)\,\mathrm dt = \frac12\sec(t)\tan(t) + \frac12\ln\left|\sec(t)+\tan(t)\right| + C`

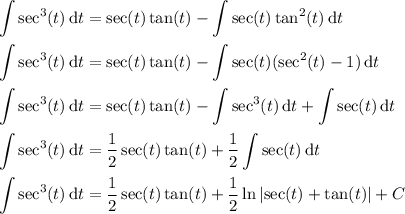
To summarize, if I denotes the original integral, we have

`\displaystyle I = \frac12x^2 - \int√(x^2-1)\,\mathrm dx \\\\ I = \frac12x^2 - \int\sec(t)\tan^2(t)\,\mathrm dt \\\\ I = \frac12x^2 - \sec(t)\tan(t) + \int\sec^3(t)\,\mathrm dt \\\\ I = \frac12x^2 - \sec(t)\tan(t) + \frac12\sec(t)\tan(t) + \frac12\ln\left|\sec(t)+\tan(t)\right| + C \\\\ I = \frac12x^2 - \frac12\sec(t)\tan(t) + \frac12\ln\left|\sec(t)+\tan(t)\right| + C`

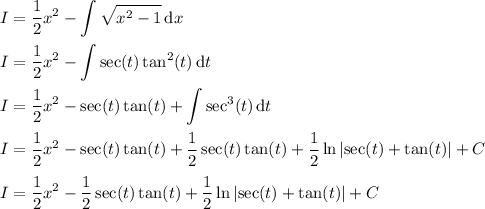
Putting everything back in terms of x, we have

sec(t ) = x

tan(t ) = √(x ² - 1)

so that

`\displaystyle I = \boxed+C`