In any artihmetic sequence, consecutive terms differ by a fixed constant c. So given the first term a, the second term is a + c, the third terms is a + 2c, and so on, up to the n-th term a + (n - 1)c.
If the 15th term is 40, then
40 = -12 + (15 - 1) c ==> c = 52/14 = 26/7
We can then write the n-th term as
-12 + (n - 1) 26/7 = (26n - 110)/7
The sum of the first 15 terms is then
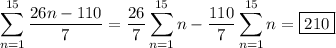
Another way to compute the sum: let S denote the sum,
S = -12 - 58/7 - 32/7 + … + 228/7 + 254/7 + 40
Reverse the order of terms:
S* = 40 + 254/7 + 228/7 + … - 32/7 - 58/7 - 12
Notice that adding up terms in the same position gives the same result,
-12 + 40 = 28
-58/7 + 254/7 = 28
-32/7 + 228/7 = 28
so that
S + S* = 2S = 28 + 28 + 28 + … + 28 + 28 + 28
There are 15 terms in the sum, so
2S = 15×28 ==> S = 15×28/2 = 210