Answer:
(b) It is symmetrical about
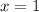
Explanation:
Given
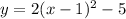
See attachment for options
Required
True statement about the graph
First, we check the line of symmetric
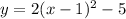
Expand
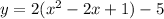
Open bracket
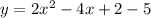
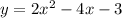
A quadratic equation
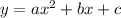 has the following line of symmetry
has the following line of symmetry
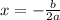
By comparison, the equation becomes:
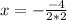
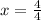
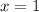
Hence, the line of symmetry is at:
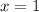
(b) is true.