Answer:
Approximately
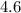 .
.
Step-by-step explanation:
Hypochlorous acid
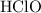 ionizes partially at room temperature:
ionizes partially at room temperature:
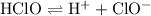 .
.
The initial concentration of
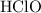 in this solution is
in this solution is
 .
.
Construct a
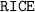 table to analyze the concentration (also in
table to analyze the concentration (also in
 ) of the species in this equilibrium.
) of the species in this equilibrium.
The initial concentration of
 is negligible (around
is negligible (around
 ) when compared to the concentration of
) when compared to the concentration of
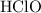 .
.
Let
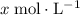 be the reduction in the concentration of
be the reduction in the concentration of
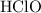 at equilibrium when compared to the initial value. Accordingly, the concentration of
at equilibrium when compared to the initial value. Accordingly, the concentration of
 and
and
 would both increase by
would both increase by
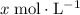 . (
. (
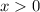 since concentration should be non-negative.)
since concentration should be non-negative.)
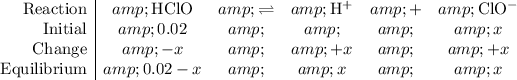 .
.
Let
![\rm [H^(+)]](https://img.qammunity.org/2022/formulas/chemistry/college/dd1xl7ld3cyesfxepcyvjgk0g0i0wqktp1.png) ,
,
![\rm [ClO^(-)]](https://img.qammunity.org/2022/formulas/chemistry/college/la9xr5wlzgu0zoamd1ptti9mhxnc0ktsv1.png) , and
, and
![[{\rm HClO}]](https://img.qammunity.org/2022/formulas/chemistry/college/sb66mag6f1k0w46dvvv38kv04fmnzcv7cv.png) denote the concentration of the three species at equilibrium respectively. Equation for the
denote the concentration of the three species at equilibrium respectively. Equation for the
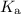 of
of
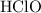 :
:
![\begin{aligned}K_\text{a} &= (\rm [H^(+)] \cdot [ClO^(-)])/([\rm HClO])\end{aligned}](https://img.qammunity.org/2022/formulas/chemistry/college/mfsetngyhpwq2fbr6a1hjxm9e7o72v7hy8.png) .
.
Using equilibrium concentration values from the
 table above:
table above:
![\begin{aligned}K_\text{a} &= (\rm [H^(+)] \cdot [ClO^(-)])/([\rm HClO]) = (x^(2))/(0.02 - x)\end{aligned}](https://img.qammunity.org/2022/formulas/chemistry/college/u5jh90r6rwml5g2ybu8aadxzsppeznlka6.png) .
.
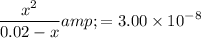 .
.
Since
 is a weak acid, it is reasonable to expect that only a very small fraction of these molecules would be ionized at the equilibrium.
is a weak acid, it is reasonable to expect that only a very small fraction of these molecules would be ionized at the equilibrium.
In other words, the value of
 (concentration of
(concentration of
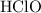 that was in ionized state at equilibrium) would be much smaller than
that was in ionized state at equilibrium) would be much smaller than
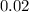 (initial concentration.)
(initial concentration.)
Hence, it would be reasonable to estimate
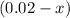 as
as
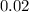 :
:
 .
.
Solve for
 with the simplifying assumption:
with the simplifying assumption:
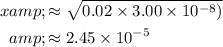 .
.
When compared to the actual value of
 (calculated without the simplifying assumption,) this estimate is accurate to three significant figures.
(calculated without the simplifying assumption,) this estimate is accurate to three significant figures.
In other words, the concentration of
 in this solution would be approximately
in this solution would be approximately
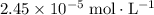 at equilibrium.
at equilibrium.
Hence the
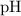 :
:
![\begin{aligned}\text{pH} &= \log_(10) ([{\rm H^(+)}]) \\ &\approx \log_(10) (2.45 * 10^(-5)) \\ &\approx 4.6\end{aligned}](https://img.qammunity.org/2022/formulas/chemistry/college/ozyfr6440llwr7tbbq1ojhgo9m37avh64f.png) .
.