Answer:
1) The kinetic energy of the object after it drops for 2.0 seconds is approximately 384.9 Joules
2) The potential energy of the object after it drops for 2.0 seconds is approximately 204 J
Step-by-step explanation:
1) The given mass of the object, m = 2.0 kg
The height from which the object is dropped, h = 30 m
The kinetic energy of the object after it drops for 2.0 seconds = Required
Kinetic energy, K.E. = (1/2)·m·v²
Where;
v = The velocity of the object
The kinematic equation for finding the velocity of the object is presented as follows;
v = u + g·t
Where;
u = The initial velocity of the object = 0
g = The acceleration due to gravity of the object ≈ 9.81 m/s²
t = The time of motion of the object = 2.0 seconds
∴ The velocity after 2 seconds, v ≈ 0 + 9.81 m/s² × 2 s = 19.62 m/s
The kinetic energy, K.E. after 2 seconds as the object drops is given as follows;
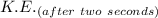= (1/2) × 2.0 kg × (19.62 m/s)² = 384.9444 J ≈ 384.9 J
2) The total energy, M.E. of the object at the top, h = 30 m, u = 0, is given as follows;
The total mechanical energy, M.E. = P.E. + K.E.
M.E. = m·g·h + (1/2)·m·u²
∴ M.E. = 2.0 kg × 9.81 m/s² × 30 m + 0 = 588.6 J
M.E. = 588.6 J
Given that the total mechanical energy, M.E., is constant, we have;
At 2.0 seconds, M.E. = 588.6 J , K.E. ≈ 384.9 J, P.E. = M.E. - K.E.
∴ P.E. = 588.9 J - 384.9 J ≈ 204 J
The potential energy after it drops 2.0 seconds, P.E. ≈ 204 J