Answer:
a)
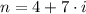 ,
,
 , b)
, b)
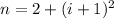 ,
,
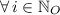
Explanation:
a) The sequence is representative for an arithmetic sequence, whose key characteristic is that difference is between two consecutive elements is the same. In particular, the sequence has a difference of 7 between any two consecutive elements and the initial element is 4. Hence, we can derive the following formula:
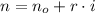 ,
,
 (1)
(1)
Where:
 - Initial element.
- Initial element.
 - Difference between two consecutive elements.
- Difference between two consecutive elements.
 - Index.
- Index.
If we know that
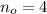 and
and
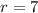 , then the expression for the n-th term of the sequence is:
, then the expression for the n-th term of the sequence is:
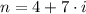 ,
,
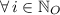
b) In this case, we have a geometric sequence described by the following equation:
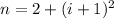 ,
,
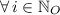 (2)
(2)
The constant element (
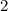 ) represents the two extreme squares, whereas the second order binomial represents the total of squares in the middle (
) represents the two extreme squares, whereas the second order binomial represents the total of squares in the middle (
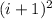 ) and emulates the area formula of the square.
) and emulates the area formula of the square.